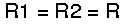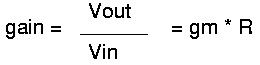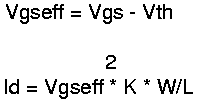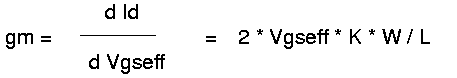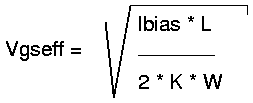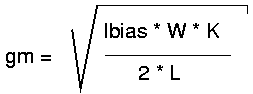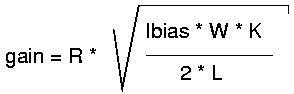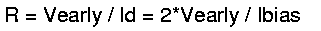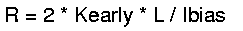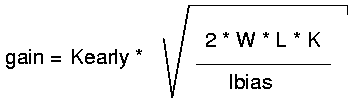Operationnal Amplifiers

(Last update November. 4 2009, Update May 12 2017)

Operational amplifiers are used in wide variety in integrated circuit design. The variety of topologies results from different application requirements such as:

    - high accuracy (also see autozero OPs too)
    - low noise
    - low current consumption
    - high speed
    - input common mode range (rail to rail)
    - output voltage swing
    - output impedance
    - response to input overdrive
    - input impedance
    - low cost
    - Instrumentation Amplifiers

Some of these design targets exclude one another or only can be achieved together at very high effort. This leads to a big variety of topologies.

The Circuits

Since the variety of topologies is so big this page will NEVER be complete. I simply add circuits as I need them for trainings.

The Basics

Opamps can be sorted by the number of gain stages. Today (2008) most common designs use 2 stages or in some cases 3 stages. Since the voltage gain drops with technologies using shorter channel length low voltage designs may even require higher numbers of stages in the future.

Single Gain Stage Amplifier

This is the most generic operational amplifier. It consists of a differential amplifier and a unity gain voltage follower. Usually the gain is low but it is very nice for learning how it works. So here it is kept as a tutorial example.
The load of the differential amplifier can be a resistor or - more frequently found - a current mirror.

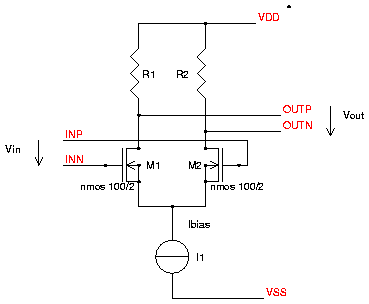
Fig. 1: Example of a Differential Stage with Resistor Load

Normally R1 and R2 are equal. So in the following we assume:

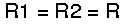
So the differential voltage gain becomes:

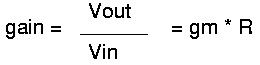
gm is the transconductance of the MOS transistors. gm depends on technology (mainly gate oxide thickness tox), temperature (carrier mobility is a function of temperature), transistor width W, transistor length L, and bias current Ibias. Technology parameters usually are hidden in the factor K.
In strong inversion the current of a MOS transistor calculates as:

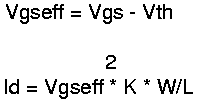
Since we need gm of one of the transistors of the differential ampliifer we have to derive this equation:

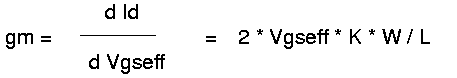
So what is Vgseff ?
Id in the balanced operating point is half of Ibias. So it can be calculated.

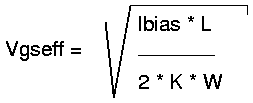
Plugging this expression into the equation of gm of one of the transistors we get:

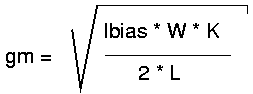
Thus the voltage gain becomes:

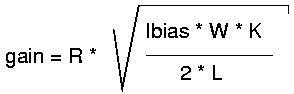
(Remark: One transistor only 'sees' half of the change of Vin but at the output Vout is differential again so we see both hafts again.)

To get a rough idea of the performance of such an amplifier let us use some numbers:
K = 50 uA/V², L=2um, W=100um, Ibias=100uA, R=100K

gain = 11.18

To increase the gain of the single stage amplifier with resistor load the following can be done:
- maximize R
- maximize W/L
- maximize Ibias
Changing Ibias or R changes the DC operating points and the required supply voltage VDD. Replacing the resistors by an active load is much more elegant.

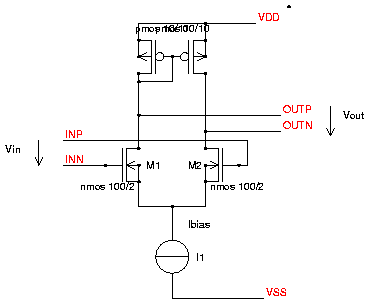
Fig. 2: Example of a Differential Amplifier with Active Load

Now node OUTN has become a current summing point with different signs for M1 and M2. Any increase of the current of M1 pulls up node OUTN. An increase of the current through M2 pulls down node OUTN. Besides that the impedance oa node OUTN is very high now because M2 as well as the PMOS transistor act as current source and current sink.
So what is the output resistance of OUTN? It now is defined by the early voltage of the shortest transistor accessing the node and the current flowing through the transistor. (to be precise: both transistor output impedances are parallel. But since the current mirror transistor usually is factors longer than the differential amplifier transistor M2 we neglect it here.)

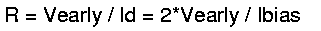
The early voltage is roughly proportional to the length of a transistor with about Kearly = 10V/um.
Neglecting the long PMOS transistors all the performance still depends on the differential stage transistors.

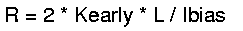
So the voltage gain in strong inversion becomes

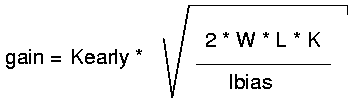
Using the same transistor parameters as before and using Kearly = 10V/um we end up with a gain of about 141 or 46dB.

To improve the gain the following can be done:
- increase L
- increase W
- reduce the bias cirrent Ibias until we reach the edge of weak inversion (here the equations change!)

Increasing W, L and reducing the bias current however makes the amplifier slow!

This simple one gain stage amplifier still is used in voltage regulators. The following figure shows the regulator amplifier of the MC1723L (taken from Motorola, Linear Integrated Circuit Data Book, 1971)

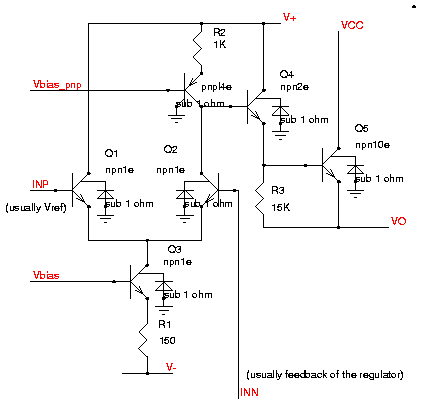
Fig. 3: Example of an actual implementation of a single gain stage OPAMP (MC723L)

Having only one gain stage the frequency compensation is fairly fool proof. This is the main reason for still using this circuit. Besides that bipolar transistors offer higher gm and better early voltages (arround 40..100V). So in bipolar technologies the single stage amplifier can be designed to reach a voltage gain of up to about 60dB.

The first publication of such a differential amplifier I am aware of dates back to 1938:
J.F. Toennies, "A Differential Amplifier", Review of Scientific Instruments, Vol. 9, March, 1938, pp 95-97.

Refinements of Single Stage Differential Amplifiers

There are several possibilities of refining the circuit to achieve higher gains at the cost of higher supply voltage or higher current consumption:
- Operation in weak inversion
- Telescopic amplifiers (traditional cascodes)
- Folded cascodes

Two Stage Operational Amplifiers

Today using two gain stages is the most common approach of designing operational amplifiers. The first (differential) stage is used as an operational transconductance amplifier (OTA) driving a second gain stage. This way the gains of both stages multiply.

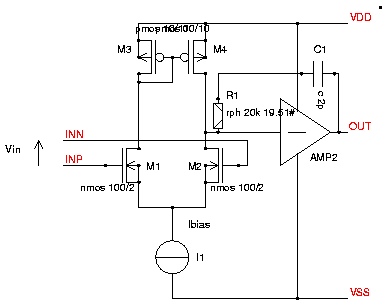
Fig. 4: Two Stage OPAMP

Since we have two gain stages now we have to take care about stability. Without C1 each stage at a certain frequency starts to act ans an integrator. So the phase shift would approach 2*90°. Feeding the signal back to the inverting input to define the closed loop gain would lead to oscillation. So there must be one dominant pole provided by the capacitor C1.
Typical examples of the two stage approach are:
    ADI model 121 (Analog Devices, 1966)
    LM101 (National Semiconductor, 1968)
    uA741 (Fairchild, 1968)
CMOS implementations like ICL7611 of Intersil were introduced a bit later arround 1976.

The most basic bipolar amplifier

This topology dates back to the 1960's. Probably the most simple and cheapest possible.

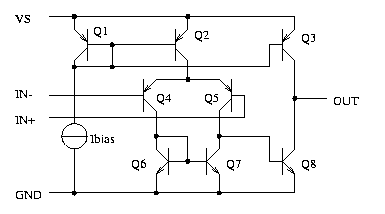
Fig. 5: The most comon bipolar opamp

Limitations of this topology are:
    - common mode range 200mV to VS-0.9V
    - PNPs are slow
    - output current capability only some uA
    - input bias current of Q4, Q5
    - only medium gain
    - not compatible with CMOS technology

The most simple CMOS opamp

Converting the bipolar circuit into a CMOS design is easy. The circuit is in use since the beginning of the 1970's.

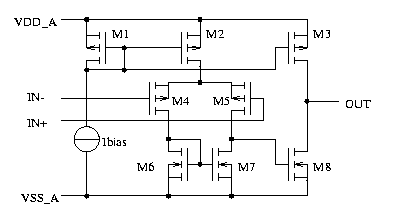
Fig. 6: simple CMOS opamp

We improved the following parameters:
    - faster because small MOS transistors have less capacities.
    - no more input bias current.
    - CMOS technology compatible

But we sacrificed other parameters compared to the previous bipolar version:
    - common mode range 200mV to VDD_A-1.5V (assuming about 0.8V threshold)
    - gate break down limit input voltage range
    - lower gain than bipolar version
    - higher offset (unless extreme sizes are used)
    - more noise

Norton amplifier

To allow higher input voltages and a wider common mode range the norton amplifier topology can be used. Bipolar counter parts exist since the 1970's (LM159, LM369)

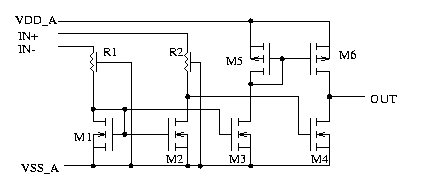
Fig. 7: norton amplifier

Now the input transistors are replaced by R1 and R2. M1 and M2 simply compare the currents flowing through R1 and R2. M4's threshold must matchthe thresholds of M1 and M2. To operate M4 at exactly the same operating point M3, M5, M6 provide exactly the same operating point. Accuracy (offset) mainly depends on the matching of R1 and R2.

Advantages:
- very cheap
- input voltage is only limited by the rupture of R1, R2

Drawbacks:
    -very poor offsets (example R1, R2 matching 0.3%, Vin versus VSS_A is 5V -> 15mV offset)
    - early voltages of M3, M4, M6 further increase offsets
    - high input bias current

3 Gain Stage Topologies

Reducing the channel length and the supply voltage the gain of the amplifier gets lower and lower. To overcome this problem the number of gain stages is further increased mainly in low voltage designs.

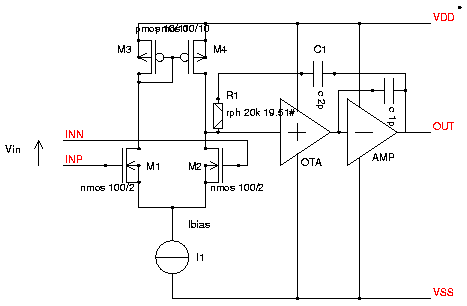
Fig. 8: Concept of an OPAMP with three gain stages

The new stage is the non inverting amplifier between the differential stage and the output stage. To keep the feedback capacitors in an affordable range (some pF) this non inverting stage usually is implemented an an OTA.
First implementations of 3 stage amplifiers are very old:

uM709 (Fairchild, 1965) is already a 3 stage design!

The concept was not estimated too much because frequency compensation of the 709 was cumbersome. But low supply voltage and short channel transistors lead to a renaissance of 3 stage amplifiers in the 1980s.

    LH0062 (National Semiconductor, 1976, used already nested miller compensation!)
    Huijsing, JSSC Dec. 1985, pp1144-1150 (uses nested miller compensation)
    OP-05 (Linear Technology, 1990, uses individual comp. of each stage)
    LT1001 (Linear Technology, 1990, nested miller compensation)